As I've mentioned elsewhere, I've implemented a bunch of different physics and inverse kinematics algorithms for games. At the 2003 Game Developers Conference, I gave a talk about 4 of the articulated rigid body simulators I prototyped for my rock climbing game, and then prognosticated about an imaginary 5th simulator that I thought would be a good direction to research for game physics.
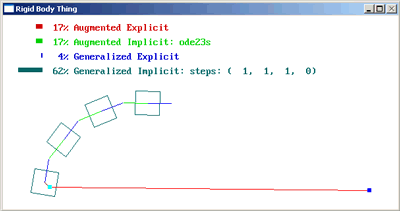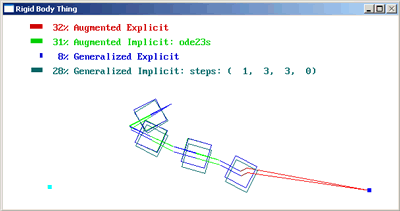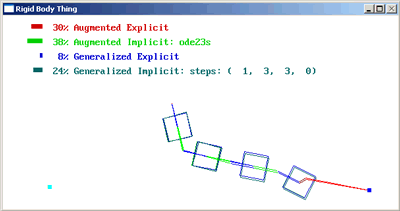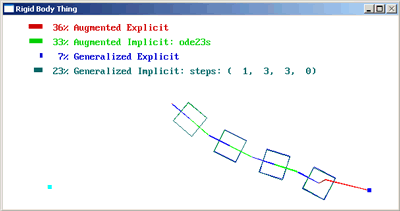
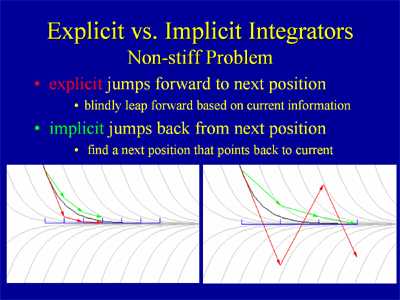
I explored two axes of the space of possible simulators, the type of integrator, whether explicit or implicit, and the type of coordinates, whether augmented or generalized:
| explicit integration | implicit integration | |
|---|---|---|
| augmented coordinates | Lagrange Multipliers | Stiff Springs |
| generalized coordinates | Composite Rigid Body Method | Recursive Newton-Euler |
The talk was titled Five Simulators for a Human Body, which was a slight misnomer, since they were really just for simulating articulated rigid bodies with stiff forces. I think the talk was not very dynamic for the attendees, but it's got a ton of subtle information about the techniques in it. I'm not sure how much of the subtlety requires you to know the material already to understand, however. This was definitely one of my "original recipe" style talks, lots of yellow text on blue backgrounds, and few pictures.
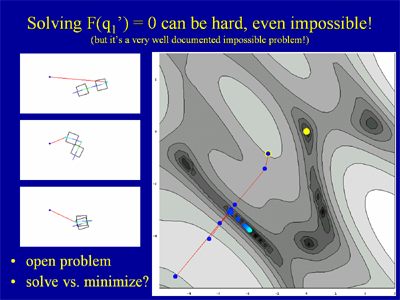
That said, in addition to the descriptions of the techniques, it's got two very important sections, one on degrees of freedom (DOF), and the other on stiffness, its importance for games, and how hard it is to solve stiff equations.
Here's the lecture abstract:
During development of the movement algorithms for an interactive dynamically animating human figure for a rock climbing game, I became dissatisfied with traditional Inverse Kinematics techniques. I turned to more advanced constrained rigid body physics algorithms to add consistency and believability. I implemented and tested four algorithms: explicit integration with Lagrange multiplier constraints, implicit integration with penalty constraints, explicit integration with the Composite Rigid Body Method, and finally implicit integration with the Recursive Newton-Euler Method. I'll cover the four algorithms, and discuss pros and cons of each, and then talk about a fifth simulation algorithm, its properties, and why it is needed to solve the simulation problem for realtime games.
The materials:
- Here are the slides. I also gave the talk in Montreal in 2004, and I think those slides are slightly better, with a few more details, but I don't have an audio recording of that, so I'm not sure you can follow along...they're mostly identical, though.
- Here is the mp3 of the talk. For some reason the actual talk doesn't start until about 1m:47s or so.